因為系上同學畢業之後，選擇繼續攻讀統計研究所的比例不少，本期系刊特闢一個主題，介紹幾所台灣目前較知名及較受大家青睞的統計研究所。全文分為四個部分，望藉由三個不同的面向：企畫小組的觀點、學長們的經驗、教授的角度，盡可能呈現統計學和統計研究所的面貌，期許讓不認識它的同學建立些許概念，讓想多認識它的同學有更進一步的了解。
文章的第一部分，我們將簡單介紹「統計學」這門科學的概貌以及簡單說明其分類；接著我們將對台灣大學、清華大學、交通大學、中央大學這四所學校的統計研究所做簡略的分析。第二部份是系友們考取統計研究所的準備和應考心得（分別是07的謝宗震、08的宋治立和張語軒，感謝他們詳盡地對應考統計研究所分享經驗和給予建議，希望提供將來要應考的學弟妹們不同於坊間的獨門心法）。最後一部份，是我們走訪中央大學、交通大學與清華大學，訪問到傅傳德教授、洪惠念教授、還有鄭少為教授，談談他們對統計的看法、比較「數學」和「統計學」這兩門學科的異同、以及對於有志往統計學領域發展的同學們的建議。
在此，衷心期望在這短短十來頁的文章中能對讀者有所助益。
Part I：什麼是統計？
統計這門學科在日常生活中廣泛被應用，甚至在國中小的課程裡也有基本統計的課程，但大家真的了解統計是什麼嗎？它在日常生活中又扮演什麼角色呢？
Statistics（統計學）最早源於現代拉丁文的statisticum collegium（國會）及義大利文的statista（國民或政治家）。而稍後德文的Statistik，最早是由Gottfried Achenwall(1749)所使用，代表對國家的資料進行分析的學問，也就是「研究國家的科學」。而其背後亦牽涉到許多數學的領域，比如機率。時至今日統計已不再僅是用在國家或政府的事務，更延伸到商業、自然、社會科學、醫療等甚至更多方面。隨著不同領域的結合，各自發展出不同的研究方法。
統計學是一門應用數學，雖然在發展時要以嚴密的理論基礎出發，但終究回歸現實。如果將統計學應用到科學、工業以及社會問題（比如：產品製程的改良、新藥的成效、股市的預測等）上。在不同的範疇上，就會有不同的母體，也就會產生不同的樣本空間，而什麼樣的樣本空間才能夠完整的呈現母體呢？簡單來說，大概是依照這樣的程序：首先，從這些樣本空間得到我們想要的數據－－這就是統計幾個重要課題之一的「抽樣方法」所要探討的－－蒐集到所需的數據之後，進一步對數據進行分析，這時，常常會為了簡化分析而將數據模型化（也就是將該組數據對應到已知的統計模型上。）藉由此一動作可以得知這個樣本空間有哪些特徵，再進一步抽取所要的資訊出來以分析母體，並由此結果判斷要如何達到目的。
隨著統計與不同領域的合作，在分析和抽樣的方法上逐漸產生一些歧異。統計學目前大約分成三個領域：工業統計、生物統計、財務統計。雖然不像數學一樣各個領域間有明顯的差異性，但三個領域間亦產生了不同點。
工業統計：
主要目標為藉由統計方法來生產「高品質、低成本」，具有競爭力的產品。因為蒐集數據的對象是工業產品，所以比較少有”missing data”（樣本在不可預料的情況下消失）的問題產生。也由於個體間的差異較小，以及可以控制的因子數目較多，所以在資料的蒐集上面可以有較多的方法可以取得，所以「實驗設計」在這塊領域有比較深入的討論。統計除了蒐集資料外還包含分析的部分，在工業統計裡所謂「可靠度分析」、「品質管制系統」就是針對製程和成品品質的改良所衍生出的學科。
生物統計：
與工業統計雖有許多類似之處，但由於研究對象從個體差異不大的無機物改成個體差異較為明顯的生物，所以在實驗進行時時常會有”missing data”及“sensor data”的產生，因此在分析時須小心此種資料是否會影響分析的結果。在臨床試驗的設計和分析是醫學上最為公眾所知的應用，比如新的藥品的效果。又如幾年前的SARS事件，民眾所接收的資訊其實大多就是流行病學或統計學的知識。
財務統計：
財務統計與前述兩個領域最大的不同點在於資料的特性和取得方式。由於財務統計所需的資料大多是已經有人整理好了數據，有些甚至不是真實存在的數據，比如股市指數、消費指數等等，所以在取得數據方面比較不需要費心，然而取得的數據大多是非獨立的，所以時間的影響對於財務統計來說具有相當程度的重要性，「時間序列分析」這門學科因應而生。財務統計的主要目標是要分析及預期整個市場的變化，藉此訓練養成專業的投資管理人才。
Part II：台灣主要的大學統計環境
台灣大學：
雖然目前沒有統計所，但若有志於統計這塊領域也是可以考慮台大數學所的統計組，方向大致上和統計研究所類似，不過在修課時可能會遇到實變數函數分析(real analysis)。此外，若對於生物統計有較濃厚興趣的同學亦可以考慮「台大公共衛生學院的流行病學研究所」的「生物醫學統計組」。
清華大學：
在清大統計研究所碩士班的學位修讀辦法裡有一條規定：碩士生入學後一年內，必須自下列學程中任選一學程(a)工業統計學程 (b)財經統計學程(c)生物統計學程。由此可知，清大會希望學生在對統計有初步認識後，能儘早投入有興趣的領域，期望學生能夠對該領域有較深入且真切的認知。此外，清大統研所裡醉心於工業統計這塊領域的教師，與其他學校相比是比較豐富的。
交通大學：
交大統計研究所的必修課程包含論文研討和專題討論，其餘基礎課程係由指導教授針對每位學生的個別情況來提出建議充實、補強所需之基礎訓練的形式。此外，藉由統計諮詢的課程可以協助學生熟悉統計方法和技巧在各界的應用。
中央大學：
除了一般常見的幾個領域外，中央統計研究所同時與中央財務金融研究所合作，共同設計了財務工程學程，是國內第一個跨系所合作之財務工程學程，對有志於財務工程相關領域的學生是一個不錯的選擇。
| 師資人數 | 成立時間(西元) |
| 專任 | 兼任 | 碩士班 | 博士班 |
| 清華大學 | 9 | 未提供 | 1988 | 1989 |
| 交通大學 | 8 | 未提供 | 1992 | 1997 |
| 中央大學 | 8 | 6 | 1979 | 1987 |
Part III：統計研究所應考心得分享
07級 謝宗震
僥倖考上清華統研，這篇是紀錄我的準備心得跟歷程，可做為對統研所感興趣的同學一個參考。我分了幾個階段，大家可以將它視為一個評量，來檢視自己的準備成效。當你不知道要如何準備時，跟著補習班的進度走是最簡易且可行的。拿各校的榜單和補習班的名單比較，會知道補習班還真的是上榜的MLE。若說我是砸錢從補習班養出來的準研究生也不盡然，除了暑假去台北補郭胖（編按：郭明慶）的數統，其他都是自修。但還是得承認有補習的那科表現得最好，大概是單科前兩名。
本篇內容的重心會擺在機率論和統計學自己準備的步調。至於重點提示如注意Chebyshev's inequality、UMVUE等，這應該是考生自己要發現的地方，這方面資訊很多，寫起來跟抄書、抄目錄沒兩樣，所以不想著墨。另外，基礎數學部份，是我在未準備完全的情況下去考試的，僅僅是依靠在數學系剩下的能力去應試，談起來頗汗顏的，就省略吧。進入正文之前先列一下我在準備期間念過的書單：
-
統計學和機率論
Introduction to Mathematical Statistics by Hogg：Chapter1~Chapter8
統計學觀念與方法（管中閔，2e）：Chapter2~Chapter13
機率論 — 重點整理（郭明慶）：全
數理統計 — 重點整理（郭明慶）：全
Statistical Inference （Casella& Berger，2e）：Chapter6~Chapter9
非讀不可 — 統計學評論（趙民德）：Chapter8~Chapter12
-
微積分
Calculus（Salas，9e）：Chapter 3、4、7、8
An Introduction to Analysis （Wade，3e）：Chapter6、7、13
微積分精粹（張正、林郁）：Chapter1~Chapter5 (後半段只看過一些)
-
線性代數
Linear Algebra（Friedberg，4e）：Chapter 3、5、6
線性代數及其應用上（黃子嘉）：全
線性代數及其應用下（黃子嘉）：Chapter7、8
若你在大三時就修完數學系的機率論、統計學了，一般來說，交大、中央統研所考試就可以應付了。若目標放在清、政、成、北大，因考題方向較偏應用，所以需要去選修外系的課，建議去修經濟系的統計學I和II，尤其在TEST ANOVA Regression等部份，自修是吃不消的。也就是說，考偏應用的統研所，補數統的效益不高。清大呢？抱歉，你必須全部都要會，不然是很難考上的。當然，光是修過學校的課，再多複習還是不足以應付考試，配合工具書來準備，是很值得推薦的一個方法。
就我而言，第一次複習是以修過課的課本為主。升大四的暑假，大約花三個禮拜把Hogg課文看完，而習題只有翻翻。接著念郭明慶的機率論、數統兩本工具書，一方面從頭念起，另一方面把日前在Hogg上讀到的重點或心得抄到工具書上，對我來說，這是提昇實力最重要的步驟，一邊抄寫一邊看工具書上的考古題。在暑假結束前，能把機率論念過80%，統計學60%就很不錯了。大約兩輪以後，原文書的必要性將會被工具書上的重點取代，爾後郭胖的機率、數統就不離身了。還有一點很多人都會發生的問題是，工具書寫得很簡陋。當然這也是要求自己把重點補上的原因，因為它真的寫得很簡便，有部份概念或題目真的會看不懂，要嘛就先跳過，不然就問強者同學、問批踢踢統計版、問Google吧。我大多是搞到自己想破頭還是不會的時候，就直接跳過，等下一輪再回來想。四上結束前，我的進度是：機率2輪、數統3.5輪、微積分0.5輪、線代0。事實上，這種進度是最低下限了，連這個都沒達到，就回火星吧。
寒假到二月底就是考古題時間，每間學校寫個四、五年就很足夠了。寫考古題的要訣就是年度的順序請由95、94年開始往前寫(我是96年度的考生)，每間學校連寫個兩年考題，出題方向也會有個大概，不過一開始寫題目，應該是幾乎都不會寫，頂多也是有題目好像看過，卻想不起來怎麼做，沒關係，翻書吧。前幾份考古題寫個五小時是很正常的，請務必把全部題目都搞清楚。當你能夠縮短到三小時的時候，各校兩個年度的考題也該寫完了(我寫的是，清交央成)。考古題時間的第二階段：做93、92年的考古題，這是最重要的階段。要知道，統計所教師大約是8位，如果是輪流出題，週期大約是3年（不過成大似乎是例外，週期是2年，還蠻穩定的）。所以說該年（96）的考題跟93、92年相關程度理當是最高的，把它當作實戰吧。寫2.5小時期間盡量別翻書，這時的平均成績大概跟日後考試非常接近了。要提醒一點，如果這些考卷中，最高分還沒到70分過，是危險的，可能需要調整唸書方向或應試心態了。考古題時間的第三階段：餘下的考古題。請訓練自己在時限內完成作答。基本上，如果之前準備夠充分，應該有80%左右的題目都是能做的，剩下的是把能做的都做對。一般來說，會80%，寫對其中80%，64分也該能錄取了。所以考前的課題是在時限內完成作答以及作答穩定度的提昇。
最後要說的是，請多報考幾間學校當作模擬考。除熟悉考試感之外，從實戰中更容易發現自己不足之處，可以有機會補強。另外，就統計來說，考試次數越多，分數將會將會呈漸進遞增的狀態喔。
08級 張語軒
我蠻推薦徐南蓉老師開的數理統計，我跟宋治立大三上時都有去修，她教得很清楚，她的上課用書《Introduction to Probability and Mathematical Statistics 2nd edition／Bain and Engelhardt》我也很推薦。關於數理統計的原文書，很多人都推薦HOGG，但HOGG第六版比第五版多了很多內容，其實考試幾乎都用不到，所以我並不是很推薦大家去讀第六版HOGG。另外，再推薦一本統計的中文書《統計學／林惠玲 陳正倉》，分上下兩冊。
我想大家都會很猶豫要不要去補習，我自己有補機率和數統。但我覺得如果在修機率統計時還學得不錯的話，其實不太需要。因為補習真的會花很多時間跟金錢，而且老師講話並不是很清楚，像我上課時就是拼命抄，然後回家再慢慢看。所以我想如果你會督促自己念書而且在唸的時候沒有太多問題，去找補習班的用書跟筆記來看看其實就可以了。
08 級宋治立
很高興能與大家分享推甄的心得和經驗。推甄是大四上開始，我在大三暑假開始準備。統研所要準備的科目有：微積分、線代、統計、機率論。這段期間我上網找尋推薦的參考書，最後去書店買了ROSS的第七版機率和HOGG的第六版數統來念。不只原文書，也可以買幾本考試用書來參考，考試用書提供的考古題，有助於了解考試的方向和重點，讀起來比較有效率。至於基礎數學（微積分、線代），我買了一本裡面都是題目的參考書，不會的地方再翻翻之前的上課用書。
到了大四上，就開始準備推甄的東西，例如成績單、審查資料之類的。推甄有一些條件，像是在校成績很重要，所以若是想要推甄的人，成績還是不要掉得太差，不然口試時很容易就會被當成把柄。清大統研所的第二階段門檻是只要有一學期進全班前20%就可以，但交大統研所進第二階段的門檻就蠻高的，若總排名沒有前10，大概就進不到口試了，所以在校成績是很重要的。其他的審查資料，比如自傳、讀書計畫，可以請教學長姐，或是參考他們留下的資料。自傳大概就是把你的大學求學過程與喜歡統計的理由紀錄下來，若能寫得很豐富，會很有成就感的。但建議準備備審資料的時間不要太久，把時間拿來唸書可能比較實際一些。今年很幸運地推上三間研究所，我把這三間的考試內容與大家分享：
-
台大數學所統計科學組：第一天筆試，下午會公佈第二天口試名單。
筆試：考兩科，基礎數學與統計，並且同時發下兩張考卷，所以分配寫考卷時間就相當重要，建議先把會的先寫完。題目稍難，大都是證明題，有興趣的人可以在台大數學系網站上找到考古題。
口試：三位口試老師，先是考生自我介紹，當時他們是跟我聊聊以後想做什麼之類的，也有同學是被問前一天考試寫錯的部分。
-
交大統計所：只有口試，無筆試。
口試：分成兩關，第一關三位老師，第二關兩位老師。
第一關：考信賴區間的觀念，變數變換。
第二關：考統計，給一個問題，問如何檢定。老師們都很好，如果你不會，他們會不斷地提示你，直到答出來為止。
-
清大統計所：早上筆試，中午公佈口試名單，下午口試。
筆試：考兩科，微積分和基本統計概念。題目是填充、是非、選擇，題目不會太艱深
困難，但觀念要非常清楚。
口試：自我介紹，看書面資料問一些問題。
有筆試的學校，若你筆試考得不錯，基本上口試不會太刁難你，但若只有口試，就要很小心了，此時平常的表達能力、統計觀念和在校成績，都是評分的重要標準。以上是我的研究所推甄心得，希望對大家有幫助。祝大家都能考上理想的研究所。
Part IV：教授小專訪
傅承德教授專訪
傅承德教授，大學時代曾醉心於代數所具有的數學之美，投身於代數幾何的領域中，現於中央大學統計研究所擔任講座教授。是什麼樣因緣讓他從代數幾何轉往統計，這個似乎與代數截然不同的領域呢？
當我們問到這個問題的時候，教授稍微思考了一下，回答說：「我大學念的是純數，幾何和代數都很好，所以當時到國外唸書時，本來也是想念純數。大三時，有位研究代數幾何的教授找我去念代數幾何。然後有位在University of Pennsylvania教書的日本教授，要帶我念代數幾何，但後來他轉去念Computer Science。之後我去服兵役，退伍後也沒有跟他們連絡。就這樣，我開始讀機率，讀完機率，然後慢慢地轉到統計的領域。」
傅承德教授的經驗其實並不算少見，目前統計相關系所大部分都是具有數學相關背景的人，此一現象會讓人覺得其實統計跟數學沒有差多少。然而統計和數學之間仍是有差異存在的，對於念純數的人而言，在某些意義下轉念統計是有些困難的。數學具有的優勢是強大的理論基礎，其所研究的主題也很少具有不確定性。但現實中少有不具模糊地帶的情況存在，而統計就是用數學去描述自然界或是社會界之中很多不確定性的東西。
對一般學數學人來說，統計比較難引起興趣，它通常不會像幾何、代數那樣有嚴謹、漂亮、簡潔的證明。但經過長時間與它相處後你會覺得，統計是個非常有力的工具，很簡單、但很有用。只是，統計並非表面所見的那麼簡單，人類對於不確定性要如何清楚敘述，是個很具挑戰性的工作。雖然統計在「概念」是困難的，但在操作上並非如此。假使有興趣的話，這會是一門極具挑戰性的學問。
統計方法大致上由以下三個主軸構成：如何取得數據，如何分析，以及如何從中獲取資訊。「蒐集」，就是如何去取得數據，通常有實驗設計以及取樣的問題。「分析」，簡言之就是對數據做一些特殊的處理，比如期望值、變異數、或是建構模型。我們由數據取得資訊，利用這些資訊就可以把不確定或不知道的東西估計出來。所以說，統計大概就是在做這些事情。不過，如之前所述，統計是個工具。所以統計有興趣的課題大多專注在那些數據本身，或者說數據的來源。因此，必須對其它領域（比如財務）有相當程度的了解，才能把統計做相關的應用。也就是說，在數據裡面獲得資訊之後，還是要回到該領域的觀點去解釋數據，以及其資訊所代表的意義。
一般而言，如果用學數學的方式來學統計，在蒐集、分析數據的能力培養上會相對地不利，但對模型的解讀倒是有一定程度的幫助。會有此一問題產生的大部分原因是在於傳統的數學訓練過度的強調邏輯，造成創造力相對的比較缺乏，這是數學系學生必須要面對的問題之一。因為統計要學的好之所以困難，不是因為學習使用的方法困難，而是培養統計的思考方式不容易，又這不是光只有在課堂上聽課就能夠學到的，需要投注時間去思考才會有所突破。
洪慧念教授專訪
「數學是一門藝術；統計是非常實用的工具」
洪慧念教授，現任教於交大統計研究所。在大學時期數學成績還算不錯，碩士班投身於代數領域，據他本人所說，他大學學得最不好的就是統計。是什麼力量使得洪教授轉而置身於統計的世界呢？
洪老師這麼說：「簡單來講，你們現在是『學數學』；畢業後要『用數學』。那數學用在哪裡？除了教書，還可以用在科學上，例如：財務、資訊、生物、工程。那數學怎麼用？這在剛從數學系畢業時，是很困難的。而統計，就是一種用數學的方法，是介於數學跟應用科學之間的媒介。它不像數學那麼講究理論的基礎，當然它有證明，只是沒那麼嚴謹，但這並不表示它是錯的。統計學家可以很嚴謹，但大部分的情形沒有必要去很嚴謹，大概對，就好了。這樣就可以迅速的應用在其它科學上面了。譬如在處理大數據時，如果你要電腦算一個十維或兩百維這種高維度的積分，其實光是十維，電腦就跑不出來了。而統計呢？它可以在短時間內，給你一個接近真值的答案，犧牲一些精確度來換取時間。所以統計大概就是這樣的一個工具。當然，統計背後也有數學的基礎，所以，用數學可以幫助你在統計上發展出很多處理資料的方法。然後再用這些方法，應用在其它應用科學上。這就是從數學，踏出去外面。
「數學應該是一門藝術；證明漂不漂亮，看起來就是不一樣。數學家喜歡看漂亮的證明，這是藝術啊，所以就要看你有沒有這個藝術天分，對不對？統計是訓練一種精神，一種對數的直覺。那統計的精神是甚麼？它告訴你如何去看data，所謂data一定有noise，一定會有誤差。統計的精神就在於如何去看待這些誤差，如何去把這些誤差弄掉，如何在不規則的一群數中找出其中的數學規則。統計所的訓練是精神上的訓練，可以說是訓練你腦子的靈活度以及對資料的直覺，讓你能夠正確解讀數據，不會亂用模型，不會用錯統計方法。
「有個故事叫瞎子摸象，這故事大家都知道。就是你摸到哪裡就是哪裡。統計也是一樣，統計就是教你如何對data從一種正確的角度去切入觀看。一組data，可以由很多不同的角度去看，統計的訓練就是讓你知道，從哪個方向看才是對的。
「譬如有人想研究甄試的時候男女是否平等。他去蒐集數據，發現社會組裡面，女生錄取率比男生高；自然組裡面，女生錄取率也比男生高。但今天有另一個人不這麼看，他把數據綜合起來看，發現男生的錄取率比女生高。這些data都是真的，沒有偽造。那怎樣看才是對的？這例子只是想說明，同樣一組data，我們用不同的角度看，可能會有不同的結論。而統計的精神，就是教你，『怎麼看才是對的』。」
洪老師認為統計這種東西，念一次不懂沒有關係，再多念一次說不定就懂了，那只是一個關卡，過了，就好了。老師對數學系的同學的建議是：從實變數函數論的「測度論」去切入統計，會比較好上手，還有，在學統計的時候，就用數學系的方法，從定義開始，把每一個統計名詞的意義（字面上的意義，而不是數學上的定義）多做思考。譬如標準差，它不像Laplace是一個人名、是為了紀念，這樣一個名詞的命名，一定有它的原因。因此你就要去想其中涵意是什麼？標準差照字面解釋似乎是「把所有數據跟平均的差再取一次平均」，但實際上計算方式卻不然。所以你也要去想，「為什麼要這樣定義？為什麼不那樣定義？這樣定義有什麼好處？」若這些東西都想通想懂了，那你的統計也就念得輕鬆愉快了！
鄭少為教授專訪
「統計─一門由數字中擷取資訊的藝術」
鄭少為教授是清華數學系89級的系友，Michigan大學的統計學博士，現於清大統計所服務，研究領域為工業統計以及實驗設計。
縱使都是數學，各領域間仍是隔行如隔山，遑論統計學與數學這兩門不同的學科。統計學與數學間的相異之處，相信同學或多或少都能感覺得到。接下來，讓我們試著把差異處說得清楚些。
人類用語言來描述這個世界，數學就是一種人類用來描述這個世界的語言。當然，統計也是。這兩種語言有什麼差別呢？相對而言，數學比較重視抽象架構；而統計，則還要關照現實層面的問題。但這並不代表統計背後沒有理論架構，統計背後是有一連串奠基於機率論上的精采理論和思路來處理數字裡的資訊。對統計學家而言，除了專注在統計理論架構的發展外，更需處理該理論架構與現實問題的接軌。統計學有理論架構層面，只是沒有數學那麼抽象；統計學也有應用層面，且不僅只是簡單的應用。簡言之，這是一門介於應用和理論之間的學科。
如果令數學家廢寢忘食的是數學的純粹之美；那究竟是甚麼東西，讓統計學家對統計學著迷呢？若我們有n組代表一個班級的同學的身高數據，想知道該班同學「大概」的高矮，有什麼可行的方法呢？我們可以對它取平均數；又，透過平均數，還可以跟其它班級做一個簡單的比較。但請注意，當我們把一個n維的數據降到一維的數字（平均數），我們得到了有興趣想了解的資訊（身高大概多高），卻也喪失了某些資訊（身高的分布）。譬如，我們不能光從一個班級的身高平均數，得知這個班級同學的身高分布，也不能知道這個班級到底是高個子多，還是矮個子多，而標準差卻能幫我們辦到這件事。又譬如有n組數據，其中有個數據很大，是其它數據的幾千倍，那這n組數據的平均數是否還是有代表性呢？
當我們利用各種n維到一維的轉換來對數據執行「擷取資訊」的動作時，我們也捨棄了某些資訊。「怎麼做」才能得到我們想要的資訊？這就是統計學很重要的一個課題了。也就是說，如果用「從數字中擷取資訊」的觀點來看統計，而不僅把它視為數學的一個分支，那統計將會展現它吸引人的風貌。
「嚴謹」是數學十分要求的重點。大家也許對「因為不夠嚴謹」而被扣分的經驗並不陌生。在這樣的訓練之下，數學系學生對邏輯演繹的嚴謹度要求就會比非數學系的人高很多，這不是壞事。然而在學習統計時，若僅專注於邏輯演繹證明，則有可能以管窺天，反而不易由大的視野來看到統計截取資訊的精彩之處。而這種「對嚴謹的堅持」，並不是那麼容易就可以修正。所以老師建議大家：多做數據分析—當你學過了一些統計方法，就直接拿現實生活裡的數據來練習。練習時要時時提醒自己「我現在要做的是擷取資訊」，時時問自己「我所用的方法，真的可以讓我得到我想要的資訊嗎？」這樣子，相信各位會有很大的進步。
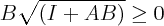，這些看起來容易，實際去解卻需要一些觀念才有辦法解釋清楚。底下列了一些我讀過的書目給大家參考：
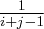)是正定矩陣等等，你會發覺，原來有這麼多有趣的結果。（p.s.此書清大館藏為失蹤，所以要到交大去借才有）
發表文章
